Let us assume the speed of the Jet = x mph.
Step 1: Given the speed of the Jet = 35mph.
Total speed of the jet with tailwind = (x+35)mph
Total speed of the jet with headwind = (x-35)mph
Step 2: To calculate using distance-time relationship
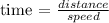

Step 3: Equate both since the two times taken for the journey are the same,
Hence

Therefore the speed of the jet = 210mph