Let's start by listing out the vertices of the rectangle BCEF
B (0, 3), C (4, -1) , E (2, -3) , F (-2, 1)
The formula for perimeter of a rectangle is given by:
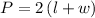
To calculate the distances BC, CE, EF & FB, we will use the formula for distance between two points:
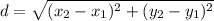
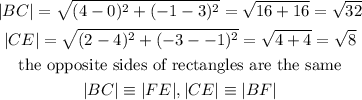
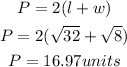
Perimeter of the rectangle BCEF is 16.97 units