Question

How would you find the slope and y-intercept of this problem and match it with a graph?

Answer 1

Given the equation:

`y=2x+1`

You can identify that it is written in Slope-Intercept Form:

`y=mx+b`

Where "m" is the slope of the line and "b" is the y-intercept.

In this case, you can identify that:

`\begin{gathered} m=2 \\ b=1 \end{gathered}`

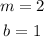
Notice that the positive slope indicates that the line rises as it moves from left to right.

By definition:

`m=(rise)/(run)`

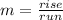
Then, you can rewrite the slope of this line as:

`m=(2)/(1)`

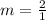
Therefore, the line moves two units up and 1 unit right.

Knowing this, you can identify its graph:

Hence, the answer is: Second option.