Question

Graph the solution set. l3x + 3l -4 < 2

Answer 1

Step 1. The inequality that we have is:

`|3x+3|-4<2`

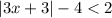
And we need to find the solution and make a graph showing the interval solution.

Step 2. First, we add 4 to both sides of the inequality to leave the absolute value alone on one side of the expression:

`\begin{gathered} |3x+3|<2+4 \\ \downarrow \\ \lvert3x+3\rvert\lt6 \end{gathered}`

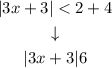
Step 3. Now we use the following rule to solve absolute value and inequality expressions:

In this case:

`\begin{gathered} \lvert3x+3\rvert\lt6 \\ \downarrow \\ -6<3x+3\lt6 \end{gathered}`

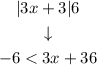
Step 4. To solve for x, subtract 3 from all of the sides of the double inequality:

`\begin{gathered} -6-3\lt3x\lt6-3 \\ \downarrow \\ -9\lt3x\lt3 \end{gathered}`

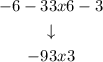
Then, divide by 3:

[tex]\begin{gathered} -\frac{9}{3}\lt x\lt\frac{3}{3} \\ \downarrow \\ \boxed{-3x can be greater than -3 but it has to be less than 1.

Step 5. Since -3 and 1 are not included in the interval, we represent them with an unfilled circle, and the rest of the interval (between -3 and 1 ) we represent it with a straight line.

Interval notation: (-3,1)

Graph:

Answer:

(-3, 1)