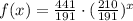Question

I need help number 5

Answer 1

A exponential function is given by:

`y=ab^x`

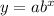
y represents the output.

a represents the initial value of the function.

b represents the rate of growth.

x represents the input.

Using the given points:

`\begin{gathered} (-2,1.91) \\ 1.91=ab^(-2)_{\text{ }}(1) \\ ------- \\ (-1,2.1) \\ 2.1=ab^(-1)_{\text{ }}(2) \end{gathered}`

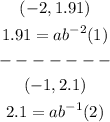
From (2) solve for b:

`b=(a)/(2.1)_{\text{ }}(3)`

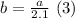
Replace (3) into (1):

`\begin{gathered} 1.91=(a)/(b^2) \\ 1.91b^2=a \\ 1.91((a)/(2.1))^2=a \\ (191)/(441)a^2=a \\ (191)/(441)a=1 \\ a=(441)/(191) \\ \end{gathered}`

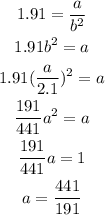
Replace a into (3):

`\begin{gathered} b=(210)/(191) \\ \end{gathered}`

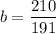
a.

b = 210/191

b.

`(210)/(191)-1=0.09948`

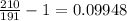
c.

`a=(441)/(191)`

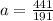
d.

`f(x)=(441)/(191)\cdot((210)/(191))^x`