Question

Find the volume of a circular cone picture below. Use 3.14 for pi. Round your answer to the nearest whole number.

Answer 1

For this problem, we are given the height and radius of the base of a cone. We need to determine the cone's volume.

A cone's volume can be calculated with the following expression:

`V=\pi r^2(h)/(3)`

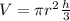
We need to apply the given data to the expression above, this is done below:

`\begin{gathered} V=3.14\cdot(28)^2\cdot(66)/(3) \\ V=3.14\cdot784\cdot22 \\ V=54159\text{ cubic meters} \end{gathered}`

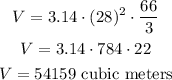
The cone's volume is equal to 54,159 cubic meters.