Question

Helium is pumped into a spherical balloon at the rate of 3pi * m ^ 3 / min . At what rate is the radius of the balloon increasing when the volume is 36pi cubic meters?

Answer 1

To find:

At what rate is the radius of the balloon increasing when the volume is 36pi cubic meters.

Solution:

It is known that the volume of the sphere is given by:

`V=(4)/(3)\pi r^3`

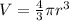
Differentiate the volume with respect to time:

`\begin{gathered} (dV)/(dt)=(4)/(3)*3\pi r^2((dr)/(dt)) \\ (dV)/(dt)=4\pi r^2((dr)/(dt)) \end{gathered}`

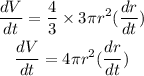
Here, given that dV/dt = 3pi, V = 36pi. First find the radius when V = 36pi.

`\begin{gathered} V=(4)/(3)\pi r^3 \\ 36\pi=(4)/(3)\pi r^3 \\ 27=r^3 \\ r=3 \end{gathered}`

Now, the rate of change of radius can be obtained as follows:

`\begin{gathered} 3\pi=4\pi(3)^2*(dr)/(dt) \\ (3\pi)/(36\pi)=(dr)/(dt) \\ (1)/(12)=(dr)/(dt) \end{gathered}`

Thus, the radius of the sphere is increasing at the rate of 1/12 m/min when the volume is 36pi.