Question

Add all of the missing information below. Descriptions should be in real-life contexts

Answer 1

Given:

The radius of the Ferris wheel is 9.5 m.

The wheel rotates fully once every 10 seconds.

Aim:

We need to find the equation that represents the height of a rider with respect to time.

Step-by-step explanation:

The form of sinusoidal eqaution is

`y=A\text{ }\cos \text{(}B(x-C))D`
`A=\frac{\text{maximum}-\text{minimum}}{2}`

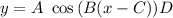
The height from the ground to the bottom of the Ferris wheel is zero.

The maximum height is 9.5+9.5 =19 m.

The minimum is 0 m.

Substitute maximum =19 and minimum =0 in equation A.

`A=(19-0)/(2)=9.5`
`B=\frac{2\pi}{P\text{eriod}}`

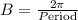
Substitute period = 10 seconds in the equation.

`B=(2\pi)/(10)=(\pi)/(5)`
`D=(Maximum+Minimum)/(2)`

Substitute maximum =19 and minimum =0 in equation D.

`D=\frac{19+0_{}}{2}=9.5m`

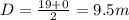
Substitute know values in the equation, we get

`y=0.5\cos \text{(}(\pi)/(5)(x-C))+9.5`

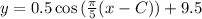
Set C=0 in the equation, we get

`y=9.5\cos \text{(}(\pi)/(5)x)+_{}9.5`

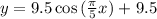
The graph of the eqaution is

The value of A should be negative.

The equation is of the form

`y=-9.5\cos \text{(}(\pi)/(5)x)+_{}9.5`

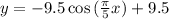
where y represents the height from the bottom of the wheel to the rider and x represents the time taken.

The x-intercepta are (10,0), (20,0) ,(30, 0 ) and so on.

The y-intecept is (0,0).

The amplitude is the exact value of A.

`|A|=|9.5|=9.5`

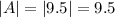
The period of the function is

`B=(\pi)/(5)`

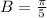
The amplitude of the given equation is 9.5.