Answer:
Option B
Step-by-step explanation:
Given that:
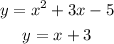
Since the right hand side of both equations are same, equate the left hand side of both the equations.
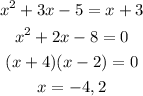
The values of x are -4 and 2.
Substitute the values of x into the equation y = x+3.
When x = -4,
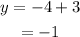
When x = 2,
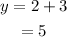
y takes the values -1 and 5. Since -1 is less than 5, the smallest value of y is -1.
So, option B is correct.