Question

Rewrite the equivalent rational expression using long division. (7p2 + 35p + 12)/(2p + 10) = ?

Answer 1

Explanation:

Given the expression:

`(7p^2+35p+12)/(2p+10)`

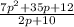
First, factor out the coefficient in the denominator.

`=(7p^2+35p+12)/(2(p+5))`

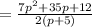
Find the zero of the denominator.

`2(p+5)=0\implies p=-5`

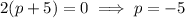
The coefficients of the numerator are: 7 35 12.

We set it in the long division table below:

Carry down the leading coefficient (7), multiply by -5, and write it in the next column. Then add.

Repeat the process until the last column.

The last value carried down (12) is the remainder.

Therefore, the result in polynomial format is:

`7p+(12)/(p+5)`

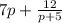
Finally, recall that we factored out 2, therefore, divide the result by 2.

`\implies(7p^2+35p+12)/(2p+10)=(7p)/(2)+(12)/(2(p+5))=(7p)/(2)+(6)/(p+5)`

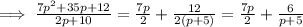
The first option is correct.