Using cosine rule
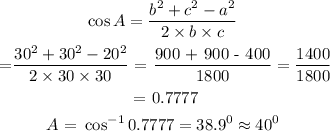
Since two sides of the triangles are equal, then the triangle is an issoseles triangle
In an issoseles triangle, two base angles are equal
This implies, angle at B = angle at C = x
Sum of angles in a triangle = 180 degrees
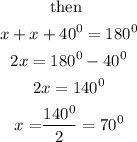
angle A = 40 degrees , angle B = 70 degrees , angle C = 70 degrees
The triangle is SAS , two sides are equal with an included angle
SSS is for triangles with equal sides