it will take 20 hours to fill the tank if both pipes are open
Step-by-step explanation:
The time it takes to fill the tank = 10 hours
In 1 hour, it will take = 1/10 hours
The time it takes for the outlet to empty the tank = 2 times the time it takes to fill the tank
The time it takes for the outlet to empty the tank = 2 × 10 = 20 hours
In 1 hour, it will take = 1/20 hours
If both pipes are open, let the time it will take to fill the tank be t hours
In 1 hour = 1/t hours
The change in the amount in the tank is equal to the time it will take to fill the tank
1/10 - 1/20 = 1/t
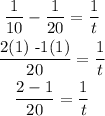
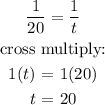
Hence, it will take 20 hours to fill the tank if both pipes are open