Question

The probability distribution for the number of students in a statistic class at RSC is given but one value is missing fill in the missing value the answer the question that follow round solution at 3 destimal places if necessary

Answer 1

The sum of all probabilities always gives 1. Then, to find the missing value:

`P(x=26)+P(x=27)+P(x=28)+P(x=29)+P(x=30)=1`

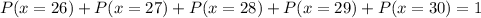
Replacing values and solving for the missing one P(x = 29):

`\begin{gathered} 0.08+0.12+0.15+P(x=29)+0.1=1 \\ P(x=29)=1-0.45 \\ P(x=29)=0.55 \end{gathered}`

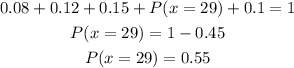
Then, the missing value is P(x = 29) = 0.55.

To find the mean number of students, we just need to multiply each x value by its probability and add all of them:

The following table shows the x values, their respective probabilities, and their product between value and probability:

xP(x) xP(x)

260.082.08

270.12 3.24

280.15 4.2

290.5515.95

300.1 3

Now, for the mean, we just need to sum all the values in the third column:

`\begin{gathered} \mu=\sum ^{}_{}x\cdot P(x) \\ \mu=2.08+3.24+4.2+15.95+3 \\ \mu=28.47 \end{gathered}`

The mean number of students in a Statistics class is 28.47.

Now, for the standard deviation, we need to estimate the square of the difference between each x-value and the mean, and multiply that value by the respective probability:

xP(x)xP(x) (x-µ)^2*P(x)

260.082.080.488072

270.12 3.240.259308

280.15 4.20.033135

290.5515.950.154495

300.1 30.23409

To find the standard deviation, we sum all the values in the fourth column, and calculate the square root of that sum:

`\sigma=\sqrt[]{\sum ^{}_{}(x-\mu)^2P(x)}`
`\begin{gathered} \sigma=\sqrt[]{0.488+0.259+0.033+0.154+0.234} \\ \sigma=\sqrt[]{1.168} \\ \sigma\approx1.081 \end{gathered}`

The standard deviation is approximately 1.081.