Question

Find the balance on an account if you invest $863 at 6.2% for 9 years compounded monthly. Round to the nearest cent.

Answer 1

To solve this problem, we will use the formula for compound interest:

`P_N=P_0\cdot(1+(r)/(k))^(N\cdot k).`

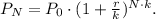
Where:

• P_N = principal amount after N years,

,

• P_0 = initial principal amount,

,

• r = interest ratio in decimals,

,

• k = compound periods per year.

In this problem, we have:

• N = 9 years,

,

• P_N = ?,

,

• P_0 = $863,

,

• r = 6.2% = 6.2/100 = 0.062,

,

• k = 12 (the inerest is compounded monthly).

Replacing these data in the formula above, we get:

`P_9=\text{ \$863 }\cdot(1+(0.062)/(12))^(9\cdot12)\cong\text{ \$1505.65.}`

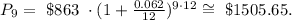
Answer

The balance after 9 years will be $1505.65 to the nearest cent.