Given in the following figure:
AB = 4.25
AC = 6.93
∠A = 84.08°
∠B = 62.86°
With the following given, for us to be able to get the area of the triangle, we will be using the following formula:
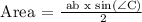
Where,
a and b are two adjacent sides of the triangle and ∠C is the angle between the two sides.
From the given, AB and AC are adjacent sides and the angle between them is ∠A.
Now, from the formula that we will be using, let:
a = AB = 4.25
b = AC = 6.93
∠C = ∠A = 84.08°
We get,
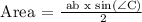
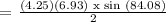
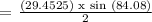
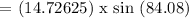
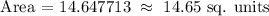
Therefore, the answer is letter D.