When two values are inversely proportional, it is true that

Then, transcribing the given statement into the mathematical language you have
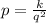
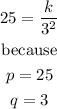
Now, you can solve for k
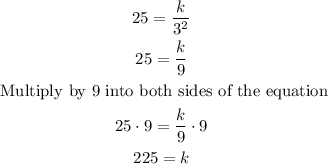
Finally, since you already have the value of k you can determine the value of p

Therefore, the value of p is 9 when q is equal to 5.