Question

Using the data in the table, what is the best prediction for the height off the ground at 25 minutes? and at 29 minutes ?

Answer 1

At 25 minutes, the height is 35.98 ft

At 29 minutes, the height is 30.98 ft.

Step-by-step explanation

We want to predict the value of the height at 25 minutes and 29 minutes.

To do this, we have to form the quadratic equation that represents the given data.

The general form of a quadratic equation is:

`\text{y = ax}^2\text{ + bx + c}`

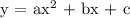
Now, what we will do is to pick several pairs of x and y from the table and find the values of a, b and c.

From the graph, the x values are time and the y values are height.

So, let us pick (x, y) = (1, 15.8):

`\begin{gathered} 15.8\text{ = a(1) + b(1) +c} \\ 15.8\text{ = a + b + c} \\ a\text{ = }15.8\text{ - b - c \_\_\_\_\_(1)} \end{gathered}`

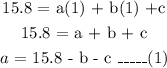
Now, pick another set of points (x, y) = (11, 58.8):

`\begin{gathered} 58.8=a(11)^2\text{ + b(11) + c} \\ 58.8\text{ = 121a + 11b + c} \\ \text{Put (1) into the equation, that is the value of a:} \\ 58.8\text{ = 121(15.8 - b - c) + 11b + c} \\ 58.8\text{ = 1911.8 - 121b - 121c + 11b + c} \\ Collect\text{ like terms:} \\ 58.8\text{ -1911.8 = -110b - 120c} \\ \text{Make b subject of formula:} \\ 110b\text{ = 1853 - 120c} \\ \text{Divide through by 110:} \\ b\text{ = 16.85 - 1.09c} \end{gathered}`

Now, pick another set of points (x, y) = (19, 59.2):

`\begin{gathered} 59.2=a(19)^2\text{ + b(19) + c} \\ 59.2\text{ = }361a\text{ + 19b + c} \\ \text{Put the value of a:} \\ 59.2\text{ = 361(15.8 - b - c) + 19b + c} \\ 59.2\text{ = 5703.8 - 361b - 361c + 19b + c} \\ \text{Collect like terms:} \\ 59.2\text{ - 5703.8 = -342b -360c} \\ \text{Put the value of b:} \\ -5644.6\text{ = -342(16.85 - 1.09c) - 360c} \\ -5644.6\text{ = -5762.7 +372.78c - 360c} \\ \text{Collect like terms:} \\ 5762.7\text{ - 5644.6 = 372.8c - 360c} \\ 118.1\text{ = 12.8c} \\ c\text{ = }(118.1)/(12.8) \\ c\text{ = 9.23} \end{gathered}`

Now, we put another set of points and this time we put the value of c. Let us pick (x, y) = (5, 26.4):

`\begin{gathered} 26.4=a(5)^2\text{ + b(5) + 9.23} \\ 26.4\text{ = 25a + 5b + 9.23} \\ \Rightarrow25a\text{ = 26.4 -9.23 - 5b} \\ 25a\text{ = 17.17 - 5b} \\ \text{Divide through by 25:} \\ a\text{ = 0.69 - 0.2b} \end{gathered}`

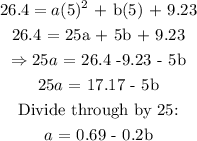
Again, we substitute another pair of points (x, y) = (15, 72.5) and the values of a and c:

`\begin{gathered} 72.5=a(15)^2\text{ + b(15) + 9.23} \\ 72.5\text{ = 225(0.69 - 0.2b) + 15b + }9.23 \\ 72.5\text{ = 155.25 - 45b + 15b + 9.23} \\ \text{Collect like terms:} \\ 45b\text{ - 15b = 9.23+ 155.25 - 72.5} \\ 30b\text{ = 91.98} \\ b\text{ = }(91.98)/(30) \\ b\text{ = 3.07} \end{gathered}`

Finally, we use the last pair of points (x, y) = (23, 36.6) and the values of b and c:

`\begin{gathered} 36.6=a(23^2\text{) + (3.07 }\cdot\text{ 23) + 9.23} \\ 36.6\text{ = }529a\text{ + 70.61 + 9.23} \\ =>\text{ 529a = 36.6 - 70.61 - 9.23} \\ 529a\text{ = -43.24} \\ a\text{ = }(-43.24)/(529) \\ a\text{ = -}0.08 \end{gathered}`

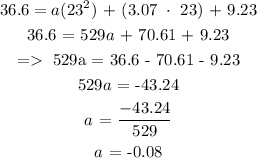
So, we have that:

a = -0.08

b = 3.07

c = 9.23

Therefore, the quadratic equation is:

`y=-0.08x^2\text{ + 3.07x + 9.23}`

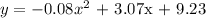
Now, we will find the height (y) when time (x) is 25 and 29 minutes:

when x = 25:

`\begin{gathered} \text{y = -0.08(25)}^2\text{ + 3.07(25) + 9.23} \\ y\text{ = -50 + }76.75\text{ + 9.23} \\ y\text{ = 35.98 }ft \end{gathered}`

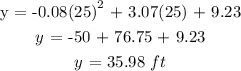
when x = 29:

`\begin{gathered} y=-0.08(29)^2\text{ + (3.07 }\cdot\text{ 29) + 9.23} \\ y\text{ = -67.28 + 89.03 + 9.23} \\ y\text{ = 30.98 ft} \end{gathered}`

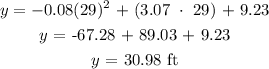
Therefore, at 25 minutes, the height off the ground is 35.98 ft and at 29 minutes, the height is 30.98 ft.