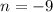The equation is given to be:
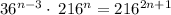
STEP 1: Rewrite each term in terms of 6.
We have that:
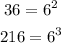
Therefore, the equation becomes:
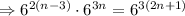
STEP 2: Apply the exponent rule:
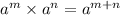
Therefore, we can have the equation to be:
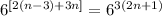
STEP 3: Compare the exponents, since the bases are the same.
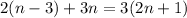
STEP 4: Expand the parentheses using the Distributive Property.
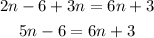
STEP 5: Subtract 5n and 3 from both sides.
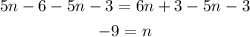
ANSWER: The answer is: