Question

The BasketballLet’s assume a basketball is dropped from a height of 1.5 m. How long will it take the basketball to reach the ground and what velocity will it reach?Problem 2 More BasketballsUse these values of initial position and initial velocity in the following questions.Initial position: ___1.0___ m above groundInitial velocity: ___6.3 __ m/s, upProblem Try to answer the following questions:(a) What is the maximum height above ground reached by the ball?(b) What are the magnitude and the direction of the velocity of the ball just before it hits the ground? Show Your Problem Solving Steps: Show these below:1) Draw a Sketch2) Choose origin, coordinate direction3) Inventory List – What is known?4) Write the kinematics equation(s) and solution of Part (a):5) Write the kinematics equation(s) and solution of Part (b):

Answer 1

We will have the following:

Problem 1.

For the first part we will calculate the time it will take to get to the ground:

`s=v_0t+(1)/(2)at^2\Rightarrow1.5m=(0m/s)t+(1)/(2)(9.8m/s^2)t^2`
`\Rightarrow t^2=(2\cdot1.5m)/(9.8m/s^2)\Rightarrow t^2=(15)/(49)s^2\Rightarrow t=\frac{\sqrt[]{15}}{7}s`
`\Rightarrow t\approx0.55s`

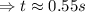
So, it will take approximately 0.55 seconds to reach the ground.

Now, we calculate the final velocity:

`v=v_0+at\Rightarrow v=(0m/s)+(9.8m/s^2)(\frac{\sqrt[]{15}}{7}s)`
`\Rightarrow v=\frac{7\sqrt[]{15}}{5}m/s\Rightarrow v\approx5.42m/s`

So, the final velocity is approximately 5.42 m/s.

1)The sketch for the problem:

2) The origin coordinate will coincide with the final position of the ball falling, that will be y = 0. And the coordinate direction will be given by a positive value for the acceleration of gravity, it will have a positive value when falling and a negative one when rising.

3) We have that the values known are:

*Original position.

*Final position.

*Initial velocity.

*Acceleration.

4) The equations to use are:

`\begin{cases}s=v_0t+(1)/(2)at^2 \\ \\ v=v_0+at \\ \\ s=(1)/(2)(v_0+v)t \\ \\ v^2=v^2_0+2as\end{cases}`

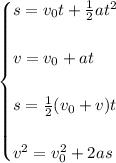
And the solution is at the begining of this problem in the answers tab.

Problem 2.

*Magnitude and direction of the acceleration as the ball goes up:

The magnitude will be of 9.8 m/s^2 and the acceleration is in direct oposition to the path the ball takes when going up.

*Magnitude an direction of the acceleration as the ball goes down:

The magnitude will be of 9.8 m/s^2 (Will not change) and in the direction the ball falls.