Given:
Probability of employees that are smokers = 35% = 0.35
Number of workers chosen random = 6
Required: Probability that there will be exactly 2 smokers
Let X denotes the number of smokers. Then X follows B(6, 0.35).
It is enough to find P(X = 2).
The binomial distribution is defined as

Substitute the given values.
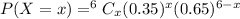
To find P(X =2), plug 2 for x .
