Question

S varies inversely as G. If S is 7 when G is 4.2, find S when G is 6.

Answer 1

The given information is:

-S varies inversely as G.

-When G is 4.2, S is 7.

As the varies inversely, then it can be expressed as:

`S=(k)/(G)`

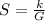
Where k is the constant of variation.

We can find k by replacing S=7 and G=4.2:

`\begin{gathered} 7=(k)/(4.2) \\ k=7*4.2 \\ k=29.4 \end{gathered}`

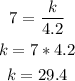
Thus, when G is 6, we can solve for S by using the constant value k:

`\begin{gathered} S=(29.4)/(6) \\ S=4.9 \end{gathered}`

The answer is when G=6, then S=4.9