Given that cot(0) = 4/3 and theta is in Quadrant I, what is sin(theta)?
we have that
If angle theta is in quadrant I , then the value of sin(theta) is positive
Remember that
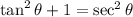
tan(theta)=1/cot(theta)
so
tan(theta)=3/4
substitute in the expression above
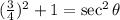
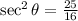

is positive because is quadrant I
remember that
sec(theta)=1/cos(theta)
so
cos(theta)=4/5
tan(theta)=3/4
tan(theta)=sin(theta)/cos(theta)
substitute given values
3/4=sin(theta)/(4/5)
sin(theta)=(3/4)*(4/5)=3/5
the answer is
sin(theta)=3/5