ANSWER
the pH of the solution is 5.02
Step-by-step explanation
Given that;
The Ka value of HCN is 6.20 x 10^-10
The concentration of HCN is 0.150M
Follow the steps below to find the pH of the solution
Step 1; Write the dissociation equation of the weak acid
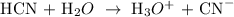
Let the dissociation of the weak acid be x
So, we have
HCN + H2O ----------->. H3O^+ + CN^-
Initial. C 0 0
Equilibrium. c(1 - x) cx cx
Step 2; Find the value of x
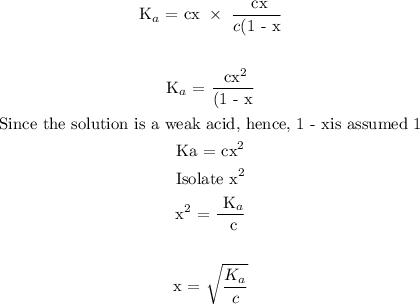
Substitute c = 0.150 and Ka = 6.20 x 10^-10 in the above formula to find x
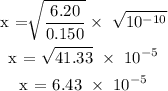
Step 3; Find the concentration of the hydroxonium ion
Recall,
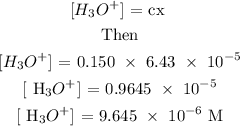
Step 4; Find the pH of the solution
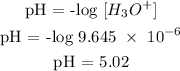
Therefore, the pH of the solution is 5.02