Question

The Ka value of HCN is Ka= 6.20 ×10–^10Calculate the pH of a 0.150 M HCN solution.

Answer 1

the pH of the solution is 5.02

Step-by-step explanation

Given that;

The Ka value of HCN is 6.20 x 10^-10

The concentration of HCN is 0.150M

Follow the steps below to find the pH of the solution

Step 1; Write the dissociation equation of the weak acid

`\text{ HCN + H}_2O\text{ }\rightarrow\text{ H}_3O^+\text{ + CN}^-`

Let the dissociation of the weak acid be x

So, we have

HCN + H2O ----------->. H3O^+ + CN^-

Initial. C 0 0

Equilibrium. c(1 - x) cx cx

Step 2; Find the value of x

`\begin{gathered} \text{ K}_a\text{ = cx }*\text{ }\frac{\text{ cx}}{c(1\text{ - x\rparen}} \\ \\ \text{ K}_a\text{ = }\frac{\text{ cx}^2}{(1\text{ - x\rparen}} \\ \text{ Since the solution is a weak acid, hence, \lparen1 - x\rparen is assumed 1} \\ \text{ Ka = cx}^2 \\ \text{ Isolate x}^2 \\ \text{ x}^2\text{ = }\frac{\text{ K}_a}{\text{ c}} \\ \text{ } \\ \text{ x = }\sqrt{(K_a)/(c)} \end{gathered}`

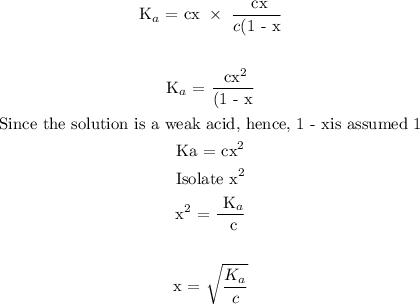
Substitute c = 0.150 and Ka = 6.20 x 10^-10 in the above formula to find x

`\begin{gathered} \text{ x =}\sqrt{(6.20)/(0.150)}*\text{ }\sqrt{10^(-10)} \\ \text{ x = }√(41.33)\text{ }*\text{ 10}^(-5) \\ \text{ x = 6.43 }*\text{ 10}^(-5) \end{gathered}`

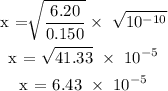
Step 3; Find the concentration of the hydroxonium ion

Recall,

`\begin{gathered} \lbrack H_3O^+\rbrack\text{ = cx} \\ \text{ Then} \\ \text{ }\lbrack H_3O^+\rbrack\text{ = 0.150 }*\text{ 6.43 }*\text{ 10}^(-5) \\ \text{ }\lbrack\text{ H}_3O^+\rbrack\text{ = 0.9645 }*\text{ 10}^(-5) \\ \text{ }\lbrack\text{ H}_3O^+\rbrack\text{ = 9.645 }*\text{ 10}^(-6)\text{ M} \end{gathered}`

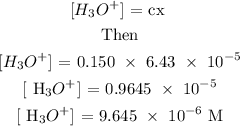
Step 4; Find the pH of the solution

`\begin{gathered} \text{ pH = -log }\lbrack H_3O^+\rbrack \\ \text{ pH = -log 9.645 }*\text{ 10}^(-6) \\ \text{ pH = 5.02} \end{gathered}`

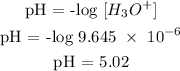
Therefore, the pH of the solution is 5.02