Question

4 pointsA photographer charges a travel fee plus an additional rate per minute.The table shows the linear relationship between the number of minutes ofa photography session and the total cost including the travel fee.Photography SessionsNumber ofTotal CostMinutes15$52.5030$75.0045$97.5060$120.0090$165.00Which statement is true?The travel fee is $52.50None of the statements are true.All the statements are true.The additional fee per minute of the photography session is $0.50.The additional fee per minute of the photography session is $3.50.The travel fee is $30.00o

Answer 1

The first thing to note is that the relationship is linear. It means that the difference between any consecutive total costs is the same: In this case, such difference is $22.5. After considering the travel fee in the first 15 mn, additional minutes don't depend on the travel fee (because it's fixed). This implies that this $22.5 from the 15 mn to 30mn is just by the additional rate. Thus, the additional rate (A) per minute is

`A=(22.5)/(15)=\text{ \$}1.5`

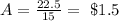
(then the options talking about the additional fee are wrong).

Now, what is the travel fee? We know the additional rate, so the travel fee (T) is

`52.50=(1.5\cdot15)+T`
`52.5-22.5=T`
`T=\text{ \$}30.00`

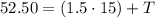
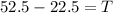
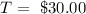
It means that the correct answer is the last.