Question

If a1 = 9 and an= an-1 + 1 then find the value of a4.

Answer 1

Since we have the recursive formula, we can find the value of a₂, a₃, and a₄.

`a_n=a_(n-1)+1\Rightarrow\text{ Recursive formula}`

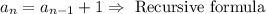
To find the value of a₂, we replace the value of a₁ in the above equation, and we operate:

`\begin{gathered} n=2 \\ a_2=a_(2-1)+1 \\ a_2=a_1+1 \\ a_2=9_{}+1 \\ a_2=10 \end{gathered}`

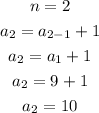
Now, to find the value of a₃, we replace the value of a₂ in the recursive formula, and we operate:

`\begin{gathered} n=3 \\ a_3=a_(3-1)+1 \\ a_3=a_2+1 \\ a_3=10+1 \\ a_3=11 \end{gathered}`

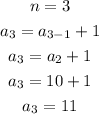
Finally, to find the value of a₄, we replace the value of a₃ in the recursive formula, and we operate:

`\begin{gathered} n=4 \\ a_4=a_(4-1)+1 \\ a_4=a_3+1 \\ a_4=11+1 \\ a_4=12 \end{gathered}`

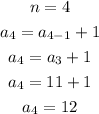
Therefore, the value a₄ is the 12.