Question

Find the vertex and the AOS for this problem f(x) = 2x^2 +12x +13

Answer 1

In order to find the vertex of this equation, we can use the formula:

`x_v=-(b)/(2a)`

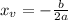
Where a and b are coefficients of the quadratic equation in the standard form:

`y=ax^2+bx+c`

Then, using a = 2 and b = 12, we have:

`x_v=-(12)/(4)=-3`

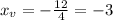
Now, to find the y-coordinate of the vertex, let's just use the value of x_v in the equation:

`\begin{gathered} f(x_v)=2\cdot(-3)^2+12\cdot(-3)+13 \\ f(-3)=2\cdot9-36+13 \\ f(-3)=18-36+13 \\ f(-3)=-5 \end{gathered}`

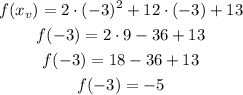
So the vertex coordinate is (-3, -5).

The axis of symmetry (AOS) is the vertical line that passes through the vertex.

So if the x-coordinate of the vertex is -3, the AOS will be x = -3.