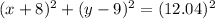Solution:
the general equation of the circle with center (h,k) and radius r is given by the following equation:
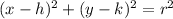
In this case, we have that:
(h,k) = (-8,9)
then, we have provisionally:
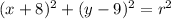
to complete this equation, we must find the radius of the circle. Note that the given circle passes through the origin, that is, the circle passes through the point (x,y)=(0,0), then, replacing these coordinates into the above equation, we get:
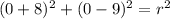
this is equivalent to:
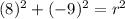
this is equivalent to:
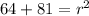
this is equivalent to:
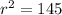
solving for r, we get:
![r=\sqrt[]{145}=\text{ 12.04}](https://img.qammunity.org/2023/formulas/mathematics/college/rhia51quyjzogwxjn1tfwby9p6tev3tiso.png)
so that, we can conclude that the equation in the general form of the given circle would be: