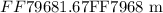We will investigate how to apply ratios in real life situations.
We are given that Edward who is ( H ) meters tall casts a shadow of certain length ( L ) as follows:

And at the same time Bella casts a shawdow of length ( L ) as follows:
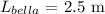
We first need to determine the relation between the Height ( H ) of a person and the length L ) of the shadow casted by that person. There are many factors that vary the length of the shadow i.e time of day, season, geographical location, external factors.
Since the length of the shawdow depends on so many factors we will assume that both Bella and Edward were subected to all these factors. So they both casted their shadow in the same set of conditions.
Ruling out everything else there is only a single factor left that can apply on the length of the shadow i.e height of the person. Considering the height ( H ) it positively influences the length ( L ) of the shadow. So we can develop a generalized direct ratio between height ( H ) of the person and the length ( L ) of the shadow casted as follows:

Now we will list down the respective heights and lengths of the shadown casted by both Edward and Bella as follows:
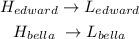
Then we will plug in the respect quantities given in the relations given above:
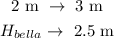
Then we will develop an equation in terms of height of Bella by cross multiplication of each entry as follows:

We have a single equation with one variable; hence, we can now solve for the height of Bella as follows:

Therefore, Bella height is as follows: