Solution:
Concept:
With the center being at the origin, the dilation formula for the shape below will be given below as
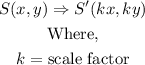
From the graph below,
The coordinates of point S is given as
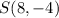
The scale factor is given as
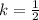
By applying the dilation formula above, we will have the coordinate of point S after dilation be
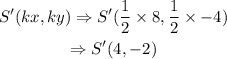
Hence,
The final answer is = ( 4, -2)