Question

ХWhat is the measure of x and y?x=76 degrees, y=10 degreesBx=76 degrees, y=20 degreesx=78 degrees, y=20 degreesx=104 degrees, y=10 degreesA+to16052°y

Answer 1

The figure shows two isosceles triangles ΔBAC and ΔBDC

A characteristic of isosceles triangles is that two of their sides are equal and that their base angles (these are the angles that make contact with only one of the two equal sides) are also equal.

Let's start with the triangle ΔBAC

As you remember, the sum of the inner angles of a triangle is 180º, given that we know two of the angles of it, we can calculate the third one as follows:

`\begin{gathered} 52+52+x=180 \\ 104+x=180 \\ x=180-104 \\ x=76º \end{gathered}`

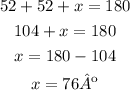
The measure of x is 76º

To determine the value of y we have to follow a similar method. ΔBDC is also isosceles so that:

Both base angles are equal, and measure yº

As before, we know that the sum of the inner angles of a triangle is 180º, so that

`y+y+160=180`

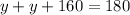
From this expression, we can calculate the value of y, first simplify the like terms

`2y+160=180`

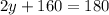
Pass 160 to the right side

`\begin{gathered} 2y=180-160 \\ 2y=20 \end{gathered}`

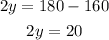
And divide both sides by 2

`\begin{gathered} (2y)/(2)=(20)/(2) \\ y=10º \end{gathered}`

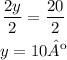
The measure of y is 10º