Given:
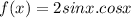
To find: Determine f'(0)=?
Step-by-step explanation:
We have given that
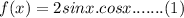
We know the identity of the trigonometric
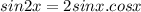
Eq.1 becomes
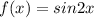
Now, differentiate f(x) w.r.to x
Therefore,
![\begin{gathered} f^(\prime)(x)=(d)/(dx)[sin(2x)] \\ \\ f^(\prime)(x)=cos2x*(d)/(dx)(2x) \\ \\ f^(\prime)(x)=cos2x*(2) \\ \\ f^(\prime)(x)=2cos2x \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/26m92tk8cqjmstxwsx8aq1psdsg9p5c2r1.png)
Hence,
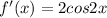
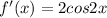
For the value of f'(0) put x = 0 in f'(x)
We get,
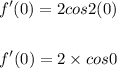
We know that
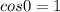
So,
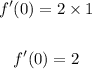
Answer: f'(0) = 2 for f(x) = 2 sin x cos x.