1 Answer

Sanchit Gupta · Answer 1 · 2023-02-15T16:07:00+0000

We will investigate how to plot straight lines on a cartesian grid by choosing values for the independent variable ( x ).

We will find 6 sets of ordered pair of cartesian coordinates for the equation:

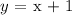
$y\text{ = x + 1}$

For this we will choose a range of values of ( x ), six in total as follows:

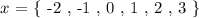
$x\text{ = }\mleft\lbrace\text{ -2 , -1 , 0 , 1 , 2 , 3 }\mright\rbrace$

To determine the corresponding values of dependent variable ( y ) we will simply plug in each value of ( x ) into the given equation and evaluate for variable ( y ).

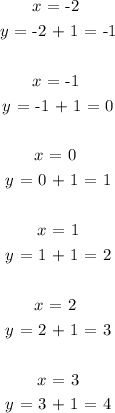
$\begin{gathered} x\text{ = -2 } \\ y\text{ = -2 + 1 = -1} \\ \\ x\text{ = -1 } \\ y\text{ = -1 + 1 = 0} \\ \\ x\text{ = 0 } \\ y\text{ = 0 + 1 = 1} \\ \\ x\text{ = }1 \\ y\text{ = 1 + 1 = 2} \\ \\ x\text{ = 2 } \\ y\text{ = 2 + 1 = 3} \\ \\ x\text{ = 3} \\ y\text{ = 3 + 1 = 4} \end{gathered}$

Hence, the 6 ordered set of cartesian coordinate pairs can be written as:

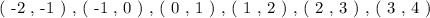
$(\text{ -2 , -1 ) , ( -1 , 0 ) , ( 0 , 1 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) }$

We will go ahead and plot each coordinate on a cartesian coordinate grid as follows:

Now we use a straight ruler and connect all the dots with a straight line. Making sure all dots lie on the line:

The next equation at hand is expressed as follows:

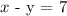
$x\text{ - y = 7}$

We will first express the above equation in the standard form i.e variables ( y ) and ( x ) separated by the " = " sign or make ( y ) the subject of the equation as follows:

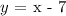
$y\text{ = x - 7}$

For this we will choose a range of values of ( x ), six in total as follows:

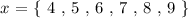
$x\text{ = }\mleft\lbrace\text{ 4 , 5 , 6 , 7 , 8 , 9 }\mright\rbrace$

To determine the corresponding values of dependent variable ( y ) we will simply plug in each value of ( x ) into the given equation and evaluate for variable ( y ).

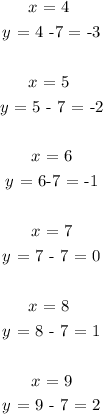
$\begin{gathered} x\text{ = 4 } \\ y\text{ = 4 -7 = -}3 \\ \\ x\text{ = 5 } \\ y\text{ = 5 - 7 = -}2 \\ \\ x\text{ = }6 \\ y\text{ = 6-7 = -1} \\ \\ x\text{ = }7 \\ y\text{ = 7 - 7 = }0 \\ \\ x\text{ = 8 } \\ y\text{ = 8 - 7 = }1 \\ \\ x\text{ = }9 \\ y\text{ = 9 - 7 = }2 \end{gathered}$

Hence, the 6 ordered set of cartesian coordinate pairs can be written as: