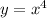Answer
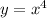
Step-by-step explanation
Problem Statement
The question gives us a polynomial:
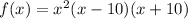
We are asked to find the end behavior of the function for large values of |x|.
Solution
To solve this question, we simply need to expand the function.
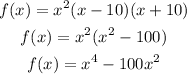
For large values of x,

Final Answer