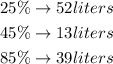Given:
There are given the chemist has three different acid solutions.
The first acid solution contains 25%.
The second contains 45%.
The third contains 85%.
Step-by-step explanation:
We need to set two-equation
So,
Let x is the amount of the 45% acid solution.
Then,
The amount of the 85% acid solution is 3x.
Since the total volume of the mixture is 104 liters.
So,
The amount of the 25% solution is:
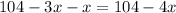
Now,
The equation for the total amount of acid in the mixture is:

Then,
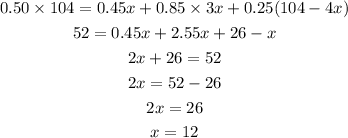
Then,
For 45%, there are 13 liters, for 85%, there are 39 liters and for 25%, there is 52 liters
Final answer:
Hence, each solution should be used: