The area of a trapezoid can be calculated with this formula:
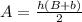
Where "A" is the area, "h" is the height, and "B" and "b" are the bases.
In this case, you can identify that:
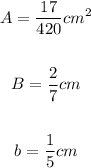
Then you can substitute these values into the formula and solve for "h". This is:
![\begin{gathered} (17)/(420)^{}=(h((2)/(7)+(1)/(5)))/(2) \\ \\ (2)((17)/(420))=h((2)/(7)+(1)/(5)) \\ \\ (17)/(210)=h((17)/(35)) \\ \\ ((17)/(210))((35)/(17))=h \\ \\ h=(1)/(6)cm \\ \\ h\approx0.2\operatorname{cm} \end{gathered}]()
The answer is:
![h\approx0.2\operatorname{cm}]()