Question

mations that has occurred.2.2A (x,y)-(-+3.y-5) C (x,y) - (x,y-5)B. (x,y) = (x+3y-5) D. (x,y) - (1-1.-y)

Answer 1

The first thing we notice is that a simple translation is no enough to get from XYZ to X'Y'Z'.

Notice that the points YZ change sides. This can be accomplished by a reflection about the y-axis.

This first transformation can be represented by:

`(x,y)\to(-x,y)`

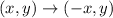
Now, we can use a translation for the rest. For this, let's choose a point of referece. Let it be X.

Point X is, at first, at (2,5). After the reflection, it get to (-2,5).

The point X' is at (1,0).

So, we need a translation to get from (-2,5) to (1,0). This can be accomplished by a translation right by 3 units and down by 5 units, which is represented by (including the previous reflection):

`(x,y)\to(-x,y)\to(-x+3,y-5)`

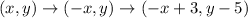
So, the complete transformation from XYZ to X'Y'Z' is:

`(x,y)\to(-x+3,y-5)`

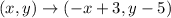
We can check to see if it works for all points:

`\begin{gathered} X=(2,5)\to(-2+3,5-5)=(1,0)=X^(\prime) \\ Y=(0,2)\to(-0+3,2-5)=(3,-3)=Y^(\prime) \\ Z=(3,1)\to(-3+3,1-5)=(0,-4)=Z^(\prime) \end{gathered}`

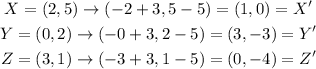
Thus, the correct option is A.