Given:
$8000 is placed in an amount that pays 17% interest compounded each year.
Required:
A) Find the amount in the account at the end of 1 year.
(B) find the amount in the account at the end of 2 years.
Step-by-step explanation:
The amount formula when interest is compound yearly is given as:
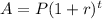
Where P = principal
r = interest rate
t = time
(a)
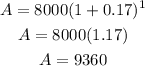
Thus the amount after 1 year is $9360.
(b)
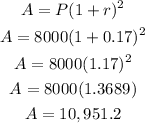
Thus the amount after 1 year is $10,951.2
Final Answer:
(a) $9360
(b) $10,951.2