Question

The right side of a tower has a shape that can be approximated by a graph of the function defined by f(x)=-304 In x/207Answer parts (a) through (c)(a) Explain why the shape of the left side of the tower has the formula given by f(-x).(b) The short horizontal line at the top of the figure has length 17.0674 feet. Approximately how tall is the tower?(c) Approximately how far from the center of the tower is the point on the right side that is 450 feet above the ground?

Answer 1

Part A; The tower is symmetric about the y- axis; therefore the left side is given by f(-x)

Part B: The tower is approximately 969 ft tall

Part C: : 47 ft

Step-by-step explanation:

Part A:

The tower is symmetric about the y-axis and we know that whenever such a symmetry exists

`f(x)=f(-x)`

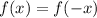
Part B:

Since we cannot evaluate the function at x = 0 to find the length of the tower, we divide the length of the top of the tower by 2 and evaluate the function at the resulting value.

`x=(17.0674)/(2)=8.5337`

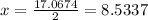
Therefore,

`f(8.5337)=-304\ln ((8.5337)/(207))`
`f(8.5337)\approx969ft`

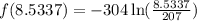
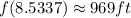
Part C:

To to find where the height is 450 ft, we solve

`450=-304\ln ((x)/(207))`

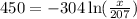
Dividing both sides by -304 gives

`-(450)/(304)=\ln ((x)/(207))`

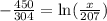
rasing both sides to the exponent of e gives

`e^{-(450)/(304)}=e^{\ln ((x)/(207))}`
`e^{-(450)/(304)}=(x)/(207)`
`0.227=(x)/(207)`

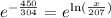
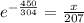
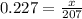
Multiplying both sides by 207 gives

`x\approx47\: ft`

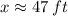
which is our answer!