Two lines are parallel if their slopes are equal. The equation of a line in slope-intercept form, is:

Where m is the slope of the line.
Write each equation in slope-intercept form to find if the slopes of each line are the same or not, which will tell us if they are parallel or not.
a)
First, isolate y from the first equation to write the equation in slope-intercept form:
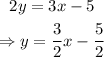
Notice that the slope of the first line is 3/2. Next, isolate y from the second equation:
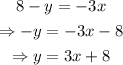
The slope of the second line is 3.
Therefore, this pair of lines is NOT parallel.
b)
Notice that both equations are already written in slope-intercept form:
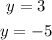
Since the variable x does not appear in the equation, this means that the coefficient of x is 0 in both cases. Then, the slope of these two lines is 0.
Therefore, this pair of lines IS parallel.