We need to find
P ( 16 < x < 26) =
In order to solve this, we need to use the following formula
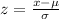
where:
mean: μ = 23.2
standard deviation: σ = 2.7
x1 = 16
x2 = 26
z is the z-score
First, we need to calculate the Z-score when x = 16 and x = 26 , then we find the probability using a z-table
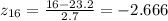
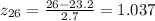
using the values above, we use the z-table and find the probability P (16[tex]\begin{gathered} P(x=16)=0.0038311 \\ P(x=26)=0.85013 \\ P(16Thus, P = 0.8463