Question

Solve d with a graph and briefly explain the transformation

Answer 1

We are given the function:

`f(x)=√(x)`

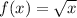
we are asked to do the following transformations:

Part A.

`g(x)=f(x+4)`

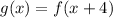
This is s transformation of the form:

`h(x)=f(x-a)`

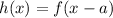
In this case, "a" is a negative number. This is a translation of the graph 4 units to the left since "a" is negative. If "a" were positive then it would be a translation to the right.

To determine the function we substitute the value of "x" in f(x) for "x + 4", like this:

`g(x)=√(x+4)`

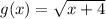
The graph of the function is:

Part B.

We are given the follwing transformation:

`g(x)=2f(2x-1)`

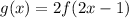
The first transformation is to stretch the function by a factor of "2", which means that we change "x" for "2x" in f(x):

`f(2x)=√(2x)`

Now, we translate the streched function 0.5 units to the right. That means that we change "2x" for "2x - 1";

`f(2x-1)=√(2x-1)`

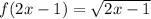
Now, we multiply the function by 2. This means that the function is stretched by a factor of 2.

`g(x)=2f(2x-1)=2√(2x-1)`

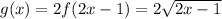
The graph of the function is the following:

Part c. In this case, this is the function translated by 1 unit to the right. The graph is the following:

Part D. This is the function translated 1 uni