Answer: We have to find the algebraic solution for the system of equations:
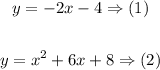
The solution is simply a point where (1) and (2) have the same coordinates, which basically means that we have to set two equations equal, therefore the solution is as follows:
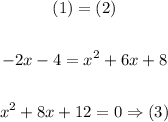
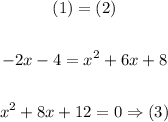
The solution to (3) is determined through a quadratic formula, the steps are as follows:
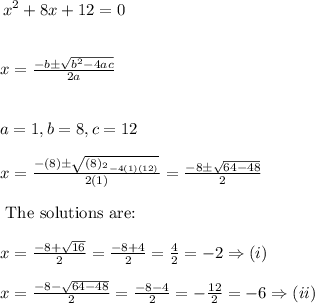
Therefore the values of the two functions at these two x values are as follows:
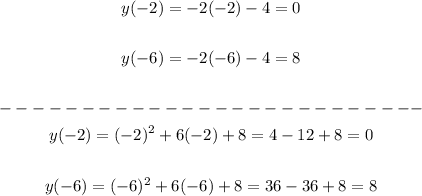
The two solutions therefore are:
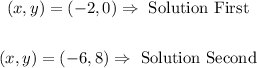
The graph confirmation: