Ellen wishes to mix candy worth $1.45 per pound with candy worth $3.74 per pound to form 27 pounds of a mixture worth $3.06 per pound.
Let x be pounds of candy worth $1.45 per pound
Then we can set up the following equation
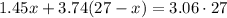
Where (27 - x) represents the pounds of candy worth $3.74 per pound
Let us solve this equation for x
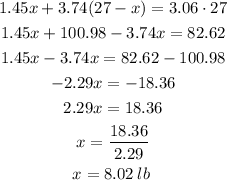
So, 8.02 pounds of less candy is required.
Whereas the pounds of more expensive candy will be

Therefore, 18.98 pounds of the more expensive candy should be used.