Question

I need to find the standard deviation of these numbers

Answer 1

We have to calculate the standard deviation of this set of numbers.

We start by calculating the mean M as:

`\begin{gathered} M=(1)/(n)\sum ^n_(i=1)\, x_i \\ M=(1)/(16)(6+6+6+6+6+5+4+4+3+3+3+3+2+2+1+0) \\ M=(60)/(16) \\ M=3.75 \end{gathered}`

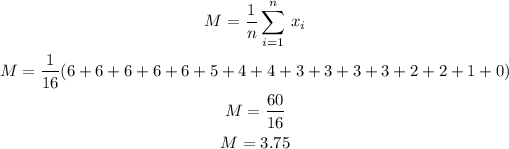
We can now calculate the standard deviation as:

NOTE: When a data is repeated we can group them in the same term with a factor that shows how many times the item repeats in the data set, like "6", that is present 5 times.

We can continue with the calculation as:

`\begin{gathered} s=\sqrt[]{(1)/(15)(5\cdot2.25^2+1.25^2+2\cdot0.25^2+4\cdot(-0.75)^2+2\cdot(-1.75)^2+(-2.75)^2+(-3.75)^2)} \\ s=\sqrt[]{(1)/(15)(5\cdot5.0625+1.5625+2\cdot0.0625+4\cdot0.5625+2\cdot3.0625+7.5625+14.0625)} \\ s=\sqrt[]{(1)/(15)(25.3125+1.5625+0.125+2.25+6.125+7.5625+14.0625)} \\ s=\sqrt[]{(57)/(15)} \\ s=\sqrt[]{3.8} \\ s\approx1.95 \end{gathered}`

Answer: The standard deviation is 1.95.