Question

A store finds that 65% of its customers pay with a credit card. If 3 customers check out, find the probability that all three of them use credit cards.

(Give your answer in the form of a decimal, to at least three digits after the decimal point.)

Answer 1

The question can be solved by using the Binomial Probability formula. This is given as

`P(X)=^nC_x.p^X.(1-p)^(n-X)`

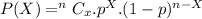
From the question, we have the following:

`\begin{gathered} n=3 \\ X=3 \\ p=0.65 \end{gathered}`

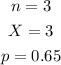
Inputting into the formula, we have

`\begin{gathered} P(X)=^3C_3*0.65^3*(1-0.65)^(3-3) \\ P(X)=(3!)/(3!(3-3)!)*0.65^3*0.35^0 \end{gathered}`

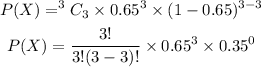
Solving further, we have

`\begin{gathered} P(X)=1*0.274625*1 \\ \therefore \\ P(X)=0.274625 \end{gathered}`

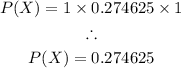
Therefore, the probability, to three decimal places, is 0.275.