We can draw a picture so we have an idea on what the question is asking.
The question tells us that the circular region that is missing has a 85° degree and that the radius of the circle is 12 ft. Then, to solve the problem we need to calculate the area of the region. We can do it using the formula
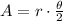
where r is the radius of the region and theta is the angle of the region in radians.
In here we have r=12 and we also have the measure of the angle is degrees. So we need to transform the angle to radians. REcall that to transform and angle from degrees to radians, we should multiply it by pi and then divide id by 180°. Lets calculate the angle in radians in our case

Then the area of the circular region is
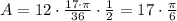
This is aproximately 8.901 square feet (taking an approximation of pi of 3.14159264)