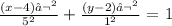Answer:
The standard form of the equation of the ellipse is:
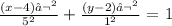
Step-by-step explanation:
Here, we want to find the equation of the ellipse
The general form equation of an ellipse with center (h,k) and length of the semi-major and semi-minor axes is as follows:
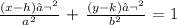
where (h,k) represents the coordinates of the center and (a,b) represents the lengths of the semi-major and semi-minor axes
We have h = 4 and k = 2
Using the equation that takes in ellipse properties, we have it that:
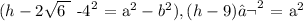
Thus, we have it that:
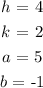
Thus, we have the standard form as: