We have to model the exponential decay of the drug quantity Q.
The time t = 0 will correspond to the moment where the dose has been injected totally.
The value of Q at time t = 0, that is Q(0), then has a value:
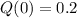
Then, the value of Q decays exponentially. The rate is 0.4% per second.
We can start expressing the general model for Q:
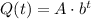
where A and b are parameters of the model.
We can find A as:
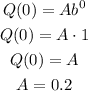
Parameter A correspond to the initial value of Q(0), which is 0.2 ml.
Now, we will use the rat of change of Q to find the parameter k.
As Q decays by 0.4% per second, we can write:
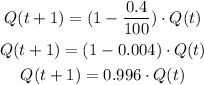
Then, we can rearrange it as:
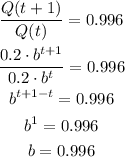
We then can express the model for Q as:
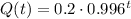
Answer: Q(t) = 0.2*(0.996)^t