Answer:
Max's carton has 2 inches squared more volume than Tucker's carton.
Explanation:
First, calculate the volume of each of the cartons.
Max's Carton
• Height = 6 inches
,
• Base Area = 12 inches squared.
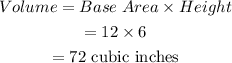
Max's carton has a volume of 72 cubic inches.
Tucker's Carton
• Height = 7 inches
,
• Base Area = 10 inches squared.
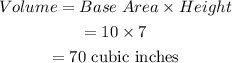
Tucker's carton has a volume of 70 cubic inches.
Next, we find the difference in volume.
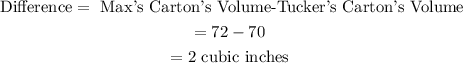
Max's carton has 2 inches squared more volume than Tucker's carton.